Logo ctfguy's blog

Pragyan 2024 - Corrupted_key

ctfguy ctfguy
February 21, 2024
0 min read
writeup crypto
Table of Contents
corrupted_key

Corrupted Key

We are given a corrupted private key. Our task was to full recover it with the partial information and use the recovered private key to ssh.

privatekey.txt

0:d=0  hl=4 l=1187 cons: SEQUENCE
4:d=1  hl=2 l=   1 prim: INTEGER           :00
7:d=1  hl=4 l= 257 prim: INTEGER           :F805C3BB46006897829ADD84A3421242DE9C0C1AC260806AFFE7C16E955CEC804A9683CCA4B607CE96AFBB4D6E55363201FAFE54A4C7FF91D4BA59D77F1B0BE35F02AB8140B8C618747ECD4C5E241F1E6C2548081EA0B52BCE84D6D24F2E981B0E7A0D46FFB41EE0B233B4C0BB5FD39061D7EC033495FF6DBDD96803674F95ADE6E34D111BE528EF055EAE9AD077DBDB0402B7A0A716EB78D524CA94C1628624EB9622CE92E0B5B9C30ED1870C6799B808C391B3CB2E3936E6B09C31C49668F7F7CD43623333F1A532E513364E511C4639CF0FE77EA3BCCA4E105E9C53485D4509BED7F661A6FBE27AE556EC63F122BB8C359D7C1E740B159947DCB9F18B88CB
268:d=1  hl=2 l=   3 prim: INTEGER         :010001
273:d=1  hl=4 l= 256 prim: INTEGER         :XXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXX
533:d=1  hl=3 l= 129 prim: INTEGER         :XXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXX
665:d=1  hl=3 l= 129 prim: INTEGER         :FC12B6905BF1D20EBE695A6FA4D46C1EABB82CB739441A5141FBBDBEF10EE757D719C8CC9882AB8D70B2C7EB79EF67D39D639D2685B44FA21FCED95A7E656429CECE26558FECE349B736D6488D7C5793CC4EECEA08F0XXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXX
797:d=1  hl=3 l= 128 prim: INTEGER         :XXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXX
928:d=1  hl=3 l= 129 prim: INTEGER         :XXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXX
1060:d=1  hl=3 l= 128 prim: INTEGER        :XXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXX

To understand about the private lets create a dummy private key using and compare with the given corrupted key.

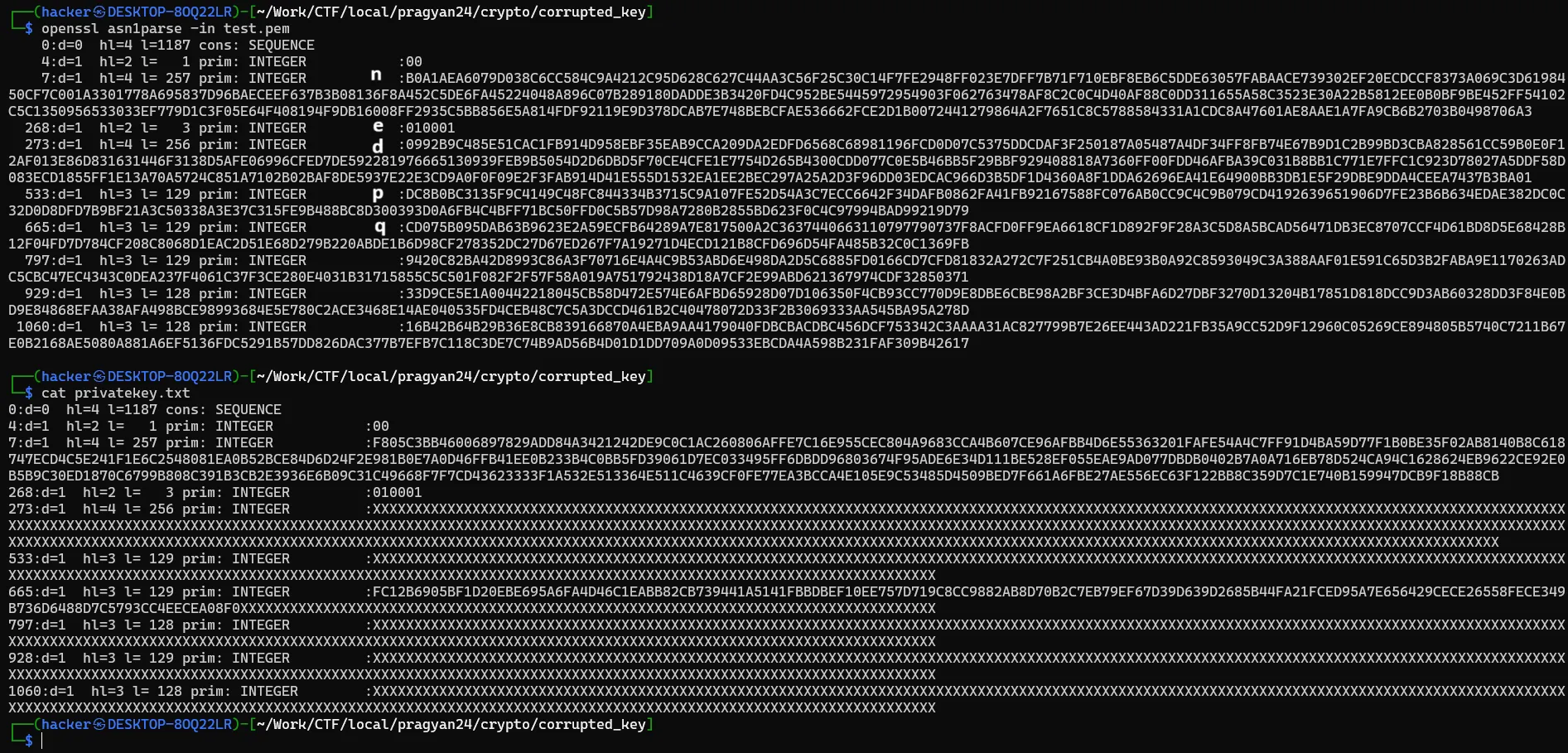
image

From the comparison we can see we have complete N,e value and a partial information about the factor of N.

We can use this information to factorize N and recover all the private keys.

Solve Script

N = 0xF805C3BB46006897829ADD84A3421242DE9C0C1AC260806AFFE7C16E955CEC804A9683CCA4B607CE96AFBB4D6E55363201FAFE54A4C7FF91D4BA59D77F1B0BE35F02AB8140B8C618747ECD4C5E241F1E6C2548081EA0B52BCE84D6D24F2E981B0E7A0D46FFB41EE0B233B4C0BB5FD39061D7EC033495FF6DBDD96803674F95ADE6E34D111BE528EF055EAE9AD077DBDB0402B7A0A716EB78D524CA94C1628624EB9622CE92E0B5B9C30ED1870C6799B808C391B3CB2E3936E6B09C31C49668F7F7CD43623333F1A532E513364E511C4639CF0FE77EA3BCCA4E105E9C53485D4509BED7F661A6FBE27AE556EC63F122BB8C359D7C1E740B159947DCB9F18B88CB
e = 0x10001
q_high = 0xFC12B6905BF1D20EBE695A6FA4D46C1EABB82CB739441A5141FBBDBEF10EE757D719C8CC9882AB8D70B2C7EB79EF67D39D639D2685B44FA21FCED95A7E656429CECE26558FECE349B736D6488D7C5793CC4EECEA08F0
P.<x> = PolynomialRing(Zmod(N))
f = q_high*(1<<336) + x
lsb = f.small_roots(X=2^400, beta=160/1024)[0]
q = q_high*(1<<336)+lsb
q = int(q)
p = N//q
d = pow(e,-1,(p-1)*(q-1))
from Crypto.PublicKey import RSA
key = RSA.construct((n,e,d,p,q))
pem = key.export_key('PEM')